Linear Discriminant Analysis in Machine Learning

Machine learning models are often used to solve supervised learning tasks, particularly classification problems, where the goal is to assign data points to specific categories or classes. However, as datasets grow larger with more features, it becomes challenging for models to process the data effectively. This is where dimensionality reduction techniques like Linear Discriminant Analysis (LDA) come into play.

LDA not only helps to reduce the number of features but also ensures that the important class-related information is retained, making it easier for models to differentiate between classes. This article explores LDA, its working principle, and its practical applications in various fields.

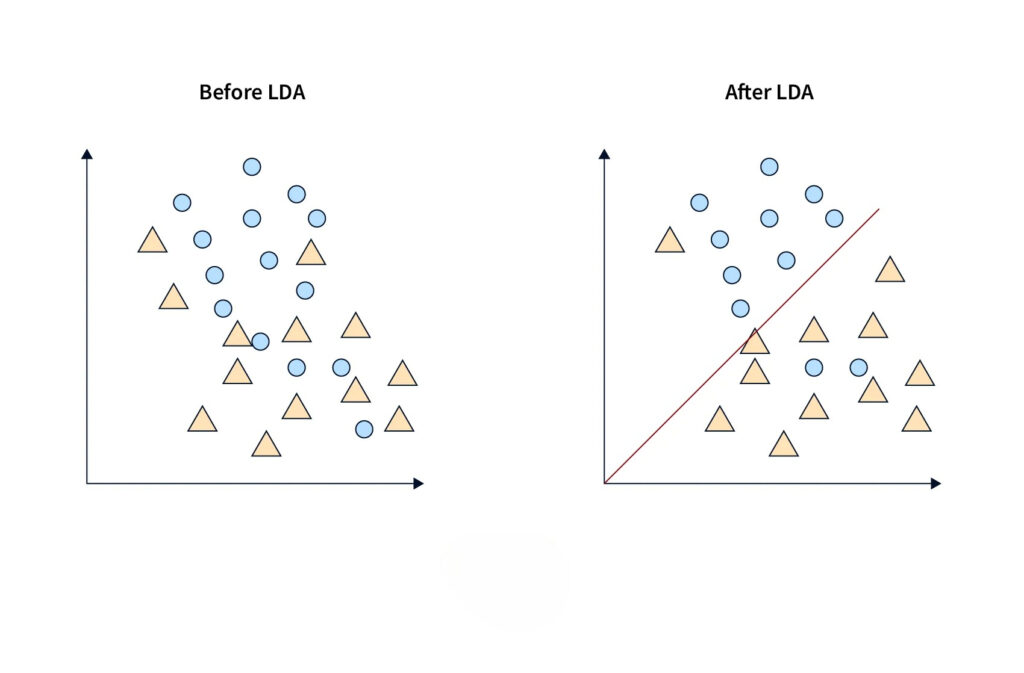
What is Linear Discriminant Analysis (LDA)

Linear Discriminant Analysis (LDA) is a supervised learning technique used for classification tasks. It helps distinguish between different classes by projecting data points onto a lower-dimensional space, maximizing the separation between those classes.

LDA performs two key roles:

1. Classification: It finds a linear combination of features that best separates multiple classes.
2. Dimensionality Reduction: It reduces the number of input features while preserving the information necessary for classification.

For example, in a dataset where each data point belongs to one of three classes, LDA transforms the data into a space where the classes are well-separated, making it easier for models to classify them correctly.

Properties and Assumptions of LDA

To perform effectively, LDA makes several key assumptions about the data:

Key Assumptions:

1. Gaussian Distribution: LDA assumes that the features within each class follow a normal (Gaussian) distribution.
2. Equal Covariance Matrices: It assumes that the variance (or spread) of data points is the same across all classes.
3. Linearity: The relationship between the features and the target variable is assumed to be linear.
4. Independence: The features used should ideally be independent of each other.

Limitations Due to These Assumptions:

• Sensitivity to Data Distribution: If the features do not follow a Gaussian distribution or if class covariances differ significantly, LDA may not perform well.
• Impact of Multicollinearity: If the input features are highly correlated, LDA’s performance may be affected.
• Limited Use with Complex Data: In datasets with complex, non-linear relationships, LDA may struggle to achieve high classification accuracy.

Preparing to Implement Linear Discriminant Analysis

Before applying LDA, it’s essential to prepare the data carefully to ensure accurate results. Below are the key steps involved in data preparation.

Steps for Data Preparation:

1. Data Cleaning: Remove any missing values or incorrect data points that could affect the results.
2. Feature Selection: Choose features that are relevant to the classification task to avoid unnecessary complexity.
3. Handling Multicollinearity: If features are highly correlated, either remove or combine them to improve LDA’s performance.
4. Feature Scaling: Although LDA is less sensitive to scaling than some other methods, applying standardization (mean=0, variance=1) can help in cases where the ranges of features vary significantly.

Carefully preparing the data ensures that the LDA model can accurately capture the relationships between the features and class labels.

How Does LDA Work?

The core idea of Linear Discriminant Analysis (LDA) is to find a new axis that best separates different classes by maximizing the distance between them. LDA achieves this by reducing the dimensionality of the data while retaining the class-discriminative information.

Key Concepts:

1. Maximizing Between-Class Variance: LDA maximizes the separation between the means of different classes.
2. Minimizing Within-Class Variance: It minimizes the spread (variance) within each class, ensuring that data points from the same class remain close together.
3. Projection to Lower-Dimensional Space: LDA projects data onto a new axis or subspace that best separates the classes. For example, in a 3-class problem, LDA can reduce the dimensionality to 2 or even 1 while preserving class-related information.

Working Mechanism:

• Step 1: Compute the mean vectors for each class.
• Step 2: Calculate the within-class and between-class scatter matrices.
• Step 3: Solve for the linear discriminants that maximize the ratio of between-class variance to within-class variance.
• Step 4: Project the data onto the new lower-dimensional space.

Mathematical Intuition Behind LDA:

LDA works by finding a new axis that best separates the classes by maximizing the between-class variance while minimizing the within-class variance. Below is a simplified breakdown of the core concepts:

1. Compute the Mean Vectors:

Calculate the mean vector for each class and the overall mean of the entire dataset.

$m_i = \frac{1}{N_i} \sum_{x \in C_i} x \quad \text{(Mean for class } i)$

where $N_i$ is the number of samples in class $C_i$.

2. Calculate Scatter Matrices:

Within-Class Scatter Matrix ($S_W$​): Measures how far data points in the same class deviate from their class mean.

$S_W = \sum_{i=1}^{k} \sum_{x \in C_i} (x – m_i)(x – m_i)^T$

Between-Class Scatter Matrix ($S_B$): Measures how far each class mean is from the overall mean.

$S_B = \sum_{i=1}^{k} N_i (m_i – m)(m_i – m)^T$

where $m$ is the overall mean of the data.

3. Objective of LDA:

LDA tries to maximize the ratio of between-class scatter to within-class scatter to achieve maximum class separation. This is represented mathematically as:

$J(w) = \frac{w^T S_B w}{w^T S_W w}$

Here, $w$ is the projection vector that defines the new axis onto which the data points are projected.

4. Solve for the Optimal Projection Vector:

The optimal projection vector $w$ is found by solving the generalized eigenvalue problem for the matrix $S_W^{-1} S_B$

5. Project Data onto the New Axis:

Once the projection vector $w$ is found, the data points are projected onto this new axis using:

$y = w^T x$

This transformation reduces the dimensionality of the data while maintaining the class-related information.

Python Code Implementation of LDA

Below is a simple example of how to implement Linear Discriminant Analysis (LDA) using Python and the scikit-learn library. This example demonstrates the key steps: training the LDA model and using it for classification.

Code Example:

# Step 1: Import necessary libraries
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.metrics import accuracy_score

# Step 2: Load the dataset (Iris dataset)
data = load_iris()
X = data.data  # Features
y = data.target  # Target labels (Classes)

# Step 3: Split the data into training and testing sets (80% train, 20% test)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Step 4: Create and train the LDA model
lda = LinearDiscriminantAnalysis()
lda.fit(X_train, y_train)

# Step 5: Make predictions on the test set
y_pred = lda.predict(X_test)

# Step 6: Evaluate the model’s performance
accuracy = accuracy_score(y_test, y_pred)
print(f'LDA Model Accuracy: {accuracy * 100:.2f}%')

Explanation:

1. Loading the Dataset: We use the popular Iris dataset, which contains data about flowers belonging to three classes.
2. Training and Testing Split: The data is divided into training and testing sets to evaluate the model.
3. Training the LDA Model: The LinearDiscriminantAnalysis() model from scikit-learn is trained using the training data.
4. Making Predictions: The model predicts class labels for the test set.
5. Evaluating Accuracy: The accuracy of the model is calculated and printed.

Advantages & Disadvantages of Using LDA

While Linear Discriminant Analysis (LDA) is a powerful tool for classification and dimensionality reduction, it has its pros and cons.

Advantages:

1. Simplicity: LDA is easy to implement and understand, making it suitable for beginners.
2. Interpretability: It provides clear insight into how features contribute to the classification task.
3. Computational Efficiency: LDA is computationally less intensive, making it useful for large datasets.
4. Works Well with Linearly Separable Data: It performs effectively when the classes are linearly separable.

Disadvantages:

1. Sensitive to Assumptions: LDA assumes that features follow a Gaussian distribution, which may not always hold.
2. Struggles with Non-linear Relationships: It may not perform well if the data contains complex, non-linear relationships.
3. Affected by Class Imbalance: LDA can be biased toward the majority class if the class distribution is imbalanced.
4. Impact of Outliers: It is sensitive to outliers, which can affect the model’s performance.

Applications of Linear Discriminant Analysis (LDA)

LDA is widely used across various fields due to its ability to classify data effectively. Below are some key applications of LDA:

1. Face Recognition

LDA helps extract features from facial images, classifying them based on individuals. It is commonly used in biometric systems to identify or verify users.

2. Disease Diagnosis in Healthcare

LDA is used to analyze medical data for classifying diseases, such as distinguishing between different stages of cancer or predicting the presence of heart disease.

3. Customer Identification in Marketing

In marketing, LDA aids in customer segmentation by grouping customers based on their profiles, enabling targeted campaigns and personalized services.

4. Credit Risk Assessment in Finance

Financial institutions use LDA to assess credit risk by analyzing customer data to predict the likelihood of loan defaults or creditworthiness.

5. Quality Control in Manufacturing

LDA identifies defects in products by analyzing sensor data, ensuring that faulty products are detected early in the production process.

6. Campaign Optimization in Marketing

LDA helps optimize marketing campaigns by analyzing customer interactions and identifying which strategies yield the best results.

Conclusion

Linear Discriminant Analysis (LDA) is a valuable technique in machine learning, offering both classification and dimensionality reduction capabilities. Its simplicity, interpretability, and computational efficiency make it a popular choice for many applications, such as face recognition, disease diagnosis, and customer segmentation. However, LDA’s performance depends heavily on the assumptions about data distribution and may struggle with non-linear relationships or class imbalances.

Despite its limitations, LDA remains a powerful tool for tackling supervised learning tasks where data follows a linear structure. As machine learning evolves, LDA continues to play an important role in solving real-world classification problems.