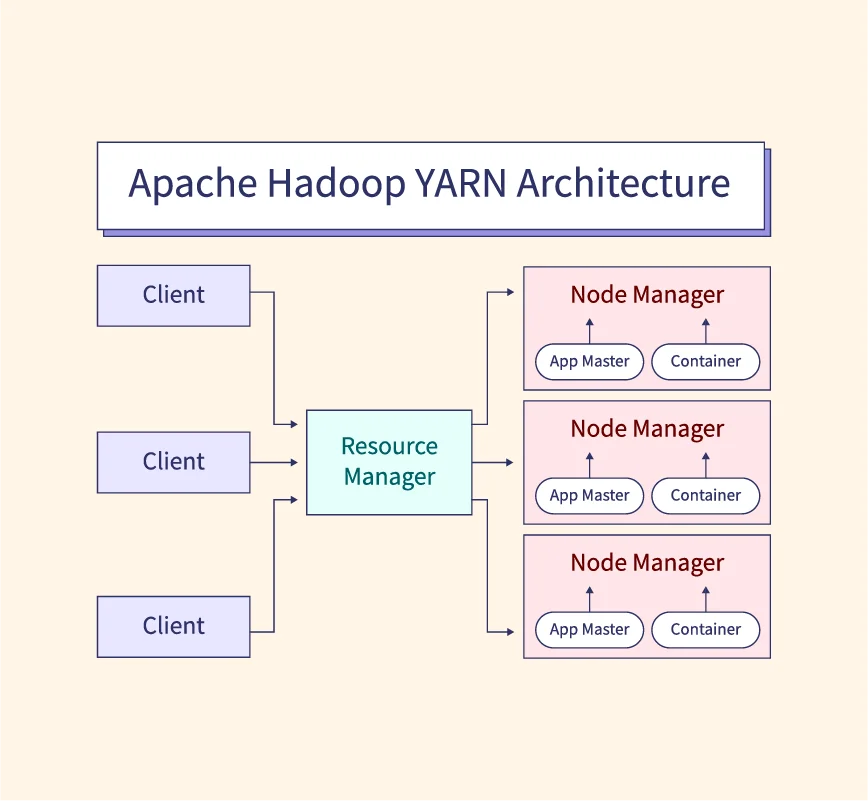
In machine learning, algorithms rely on data to learn patterns and make predictions. However, raw data is rarely ready for direct use by these models. Data preprocessing is a critical step that can significantly affect the performance of machine learning models. Among the various preprocessing techniques, feature scaling is one of the most important.
Feature scaling ensures that the numerical features of a dataset are on a similar scale, which can prevent models from being biased toward certain features simply because of their magnitudes. Without scaling, machine learning algorithms may struggle to converge or produce suboptimal results, especially for distance-based methods like k-Nearest Neighbors (k-NN) and K-Means Clustering.
In this article, we will explore what feature scaling is, why it’s essential, and the different methods you can use to scale your data.
What is Feature Scaling?
Feature scaling is the process of transforming the numerical features in a dataset to a common scale or range. In machine learning, different features in a dataset may have different ranges or units (e.g., age might range from 0 to 100, while income might range in the thousands or millions). Without scaling, these differences can cause models to weigh features unequally, leading to poor performance.
Feature scaling ensures that all features contribute equally to the model by bringing them to a similar scale. This process can involve either normalizing or standardizing the values, depending on the requirements of the algorithm and the nature of the dataset.
There are several methods for feature scaling, including:
- Normalization: Transforming values to fall within a specific range (e.g., 0 to 1).
- Standardization: Transforming features so that they have a mean of 0 and a standard deviation of 1.
- Min-Max Scaling: Scaling features to a predefined range, typically between 0 and 1.
- Robust Scaling: Scaling data based on percentiles to handle outliers more effectively.
Each method has its own strengths and is suited for different types of datasets and machine learning models.
Why Use Feature Scaling?
Feature scaling is crucial in machine learning for several reasons. Properly scaled data ensures that machine learning algorithms can perform efficiently and accurately without being biased by the range or units of different features. Here are some of the main reasons to use feature scaling:
1. Improve Algorithm Performance
Many machine learning algorithms work best when features are on a similar scale. Scaling helps models converge faster and find optimal solutions more easily. For example, in gradient descent-based algorithms, feature scaling ensures that the model updates the parameters uniformly, preventing slow convergence due to one feature dominating the learning process.
2. Optimize Distance-Based Algorithms
Algorithms that rely on distance calculations, such as k-Nearest Neighbors (k-NN), K-Means Clustering, and Support Vector Machines (SVMs), are heavily affected by the scale of features. If one feature has a much larger range than others, it will disproportionately influence the distance calculations, leading to poor clustering or classification results. Scaling ensures that all features contribute equally to the distance measure.
3. Prevent Bias from Dominant Features
In datasets with features of varying magnitudes (e.g., age vs. income), features with larger ranges can dominate the learning process, making it difficult for the model to learn from smaller features. Feature scaling helps prevent this by ensuring that no single feature disproportionately influences the model.
4. Allow Models to Treat All Features Equally
Many algorithms assume that the input features have been scaled to a similar range. Without scaling, the model may assign more importance to certain features due to their range, even if they are not necessarily more important. Feature scaling helps models weigh each feature more equally, improving overall performance.
5. Make Models More Interpretable
When features are on a common scale, it becomes easier to interpret the model’s results and understand the relative importance of each feature. This is particularly useful in linear models like linear regression, where the coefficients can be interpreted as the influence of each feature on the target variable.
Methods for Feature Scaling
There are several methods available for scaling features, each with its own use case depending on the characteristics of the dataset and the machine learning algorithm being used. Below are the most common methods for feature scaling:
1. Normalization
Normalization is a scaling technique that transforms the values of features into a specific range, typically between 0 and 1. This method is useful when you want to maintain the relative distances between values while ensuring that all features are on the same scale.
Formula for Min-Max Normalization:
Where:
- x′ is the normalized value,
- x is the original value,
- Xmin and Xmax are the minimum and maximum values in the feature.
This formula ensures that all values are scaled to a range of [0, 1]. Min-Max normalization is widely used in applications like neural networks, where the inputs need to be on a standardized scale.
Python Code Example: Min-Max Normalization (Scaling to [0, 1] range)
Min-Max scaling transforms features to a specific range, typically [0, 1].
# Min-Max Scaling (Normalization)
min_max_scaler = MinMaxScaler()
scaled_data_minmax = min_max_scaler.fit_transform(data)
print("\nMin-Max Scaled Data:\n", scaled_data_minmax)Output:
Min-Max Scaled Data:
[[0. 0. 0. ]
[0.25 0.25 0.25]
[0.5 0.5 0.5 ]
[0.75 0.75 0.75]
[1. 1. 1. ]]
Explanation: The data is scaled to a range of [0, 1], using the MinMaxScaler class from scikit-learn. This method is helpful when you want to maintain the relative scale of features but transform them into a bounded range.
Advantages:
- Maintains the relationships between data points.
- Keeps all features within a defined range (0 to 1).
Disadvantages:
- Sensitive to outliers, which can skew the results if extreme values are present.
2. Standardization
Standardization transforms the features so that they have a mean of 0 and a standard deviation of 1. This method is particularly useful when the dataset contains features with varying units or when the algorithm assumes normally distributed data.
Formula for Standardization (Z-score normalization):
Where:
- x′ is the standardized value,
- x is the original value,
- μ is the mean of the feature,
- σ is the standard deviation of the feature.
Standardization ensures that all features are centered around zero and scaled based on their variance. This method is commonly used in algorithms like Principal Component Analysis (PCA) and Logistic Regression.
Python Code Example: Standardization (Z-Score Normalization)
Standardization scales features so that they have a mean of 0 and a standard deviation of 1.
# Standardization (Z-Score Normalization)
standard_scaler = StandardScaler()
scaled_data_standard = standard_scaler.fit_transform(data)
print("\nStandard Scaled Data (Z-score normalization):\n", scaled_data_standard)
Output:
Standard Scaled Data (Z-score normalization):
[[-1.41421356 -1.41421356 -1.41421356]
[-0.70710678 -0.70710678 -0.70710678]
[ 0. 0. 0. ]
[ 0.70710678 0.70710678 0.70710678]
[ 1.41421356 1.41421356 1.41421356]]Explanation: We use StandardScaler to scale the data so that each feature has a mean of 0 and a standard deviation of 1. This is useful for algorithms like linear regression and PCA.
Advantages:
- Less affected by outliers compared to normalization.
- Works well with algorithms that assume normally distributed data.
Disadvantages:
- May distort relationships in the data if the original distribution is not close to normal.
3. Min-Max Scaling
Min-Max scaling is similar to normalization but focuses on scaling features to a specific range, which is often [0, 1]. This method is ideal when you need to maintain the relative distances between features while standardizing their scale.
Formula for Min-Max Scaling:
This is the same formula used in normalization, and it scales all feature values to the [0, 1] range. It’s a common technique in image processing and deep learning models, where features need to be scaled uniformly.
Python Code Example: Min-Max Scaling (Scaling to a Custom Range)
Min-Max scaling can be applied to scale features to any custom range. Here we’ll scale the features to a [5, 10] range.
# Min-Max Scaling to a custom range [5, 10]
min_max_scaler_custom = MinMaxScaler(feature_range=(5, 10))
scaled_data_minmax_custom = min_max_scaler_custom.fit_transform(data)
print("\nMin-Max Scaled Data (Custom Range [5, 10]):\n", scaled_data_minmax_custom)
Output:
Min-Max Scaled Data (Custom Range [5, 10]):
[[ 5. 5. 5. ]
[ 6.25 6.25 6.25]
[ 7.5 7.5 7.5 ]
[ 8.75 8.75 8.75]
[10. 10. 10. ]]
Explanation: Instead of scaling the data between [0, 1], this example scales the data between a custom range [5, 10].
Advantages:
- Simple and easy to implement.
- Maintains the relative relationships between data points.
Disadvantages:
- Sensitive to outliers, which can impact the scaling process.
4. Robust Scaling
Robust Scaling is a method designed to handle outliers more effectively than normalization or standardization. Instead of using the mean and standard deviation, robust scaling is based on percentiles like the median and the interquartile range (IQR). This method ensures that the scaling is less influenced by extreme values.
Formula for Robust Scaling:
Where:
- The median is the middle value of the feature,
- The IQR (Interquartile Range) is the range between the 25th and 75th percentiles.
Robust scaling is ideal for datasets with significant outliers, as it reduces the impact of extreme values on the scaled features.
Python Code Example:
# Robust Scaling
robust_scaler = RobustScaler()
scaled_data_robust = robust_scaler.fit_transform(data)
print("\nRobust Scaled Data (based on median and IQR):\n", scaled_data_robust)Output:
Robust Scaled Data (based on median and IQR):
[[-1.5 -1.5 -1.5]
[-0.5 -0.5 -0.5]
[ 0. 0. 0. ]
[ 0.5 0.5 0.5]
[ 1.5 1.5 1.5]]
Explanation: This scaling method is resistant to outliers by using the median and the interquartile range for scaling, instead of the mean and standard deviation.
Advantages:
- Effectively handles outliers by scaling based on percentiles.
- Suitable for non-Gaussian distributions.
Disadvantages:
- Can still be sensitive to extreme outliers, though less so than other methods.
When to Scale Your Data?
Feature scaling is not always necessary for all machine learning algorithms, but in many cases, it can significantly improve performance. Below are some scenarios where feature scaling is highly recommended:
1. Algorithms Sensitive to Feature Scale
Certain machine learning algorithms rely heavily on the scale of features to perform optimally. These include:
- k-Nearest Neighbors (k-NN): This algorithm calculates the distance between data points, and if one feature has a larger range than others, it will dominate the distance calculations.
- K-Means Clustering: Similar to k-NN, K-Means clustering relies on distance calculations. If the features are not scaled, clusters may be distorted.
- Support Vector Machines (SVMs): SVMs attempt to find the optimal hyperplane to separate classes. If the features are on different scales, the model might be biased toward features with larger ranges.
- Gradient Descent Algorithms: In algorithms like Linear Regression or Logistic Regression, gradient descent is used to minimize the loss function. If the features are not scaled, the algorithm may take longer to converge or may not converge at all.
2. Features with Vastly Different Ranges
When features in a dataset have significantly different ranges (e.g., age in years vs. income in thousands of dollars), scaling is important to ensure that the model does not place too much emphasis on the features with larger magnitudes. For example, income might range in the thousands, while age ranges from 0 to 100. Without scaling, the model may assume that income is a more important feature simply because of its larger values.
3. Distance-Based or Similarity-Based Algorithms
Algorithms that rely on distance or similarity metrics, such as cosine similarity or Euclidean distance, benefit from scaling. If the features are not on the same scale, the distance metric will be skewed by the feature with the larger range, leading to suboptimal results.
4. Neural Networks and Deep Learning Models
Neural networks, especially deep learning models, perform better when the input data is scaled. If features have vastly different scales, the model might struggle to find an optimal solution, leading to slower training and lower performance. Many deep learning frameworks recommend scaling the input features to a range of [0, 1] or [-1, 1].
5. Principal Component Analysis (PCA)
In Principal Component Analysis (PCA), the goal is to reduce dimensionality while retaining the most important variance in the dataset. Since PCA is sensitive to the magnitude of features, scaling is crucial to ensure that features with larger variances do not dominate the principal components.
When Scaling Your Data is NOT Necessary?
While feature scaling is important in many scenarios, it’s not always required. Some machine learning algorithms are not affected by the scale of the data. Below are cases where feature scaling might not be necessary:
1. Tree-Based Algorithms
Algorithms such as decision trees, random forests, and gradient boosting do not require feature scaling. These algorithms are based on decision rules, and the split points in decision trees are invariant to the scale of the data. For example:
- Decision Trees: These models split the data based on feature values, and the range of the feature does not affect the decision rules.
- Random Forests: Since random forests are an ensemble of decision trees, they also don’t need scaled features.
- Gradient Boosting: Similarly, boosting algorithms like XGBoost and LightGBM rely on decision trees, so feature scaling is not necessary.
2. Rule-Based Algorithms
Algorithms like rule-based classifiers or rule-based regression models typically do not require scaling because they operate by applying logical conditions to the input data, which are not influenced by feature magnitudes.
3. Naive Bayes
The Naive Bayes algorithm assumes that features are conditionally independent given the class label, and it calculates the probability of each feature independently. Since these probabilities are not influenced by the magnitude or range of the features, feature scaling is not necessary for Naive Bayes.
4. Linear Models with Regularization
In some cases, models like linear regression or logistic regression with regularization (such as Lasso or Ridge regression) can work well without scaling, though scaling often improves performance. If the features are already fairly similar in range, scaling may not be strictly required.
5. Categorical Features
If your dataset contains categorical features that have been encoded (such as one-hot encoding or label encoding), scaling is not necessary for these features. Scaling should only be applied to numerical features since it makes no sense to scale categorical variables.
6. Algorithms That Use Aggregate or Statistical Measures
Algorithms that rely on aggregate measures, such as mean or median, are typically less affected by feature scales. For example, in K-Nearest Neighbors (k-NN) using a non-distance-based measure like median, scaling may not be as critical.
Summary
While feature scaling is an essential step for many machine learning algorithms, it’s not always necessary. Tree-based models, rule-based algorithms, and Naive Bayes classifiers are examples of models that can operate effectively without scaling, allowing you to focus on other aspects of preprocessing and feature engineering.