Dimensionality Reduction In Machine Learning

Dimensionality reduction is a technique used in machine learning to simplify complex, high-dimensional data. As data grows in size and complexity, it often contains many features (variables), making it challenging to process. This high-dimensional data can lead to problems like the curse of dimensionality, where the performance of models deteriorates due to too many features. Dimensionality reduction addresses this issue by transforming data into a lower-dimensional space while preserving important information. This process helps in improving model performance, reducing computation time, and enhancing data visualization

What is Dimensionality Reduction?

Dimensionality reduction is the process of transforming data from a high-dimensional space (many features) to a lower-dimensional space while retaining the essential information. The main goal is to reduce the number of features or dimensions in the dataset without losing significant data patterns or structures.

There are two primary ways to achieve dimensionality reduction:

1. Feature Selection: This approach selects a subset of the most relevant features from the original dataset based on specific criteria like importance or relevance. It doesn’t alter the features but filters out the less useful ones.
2. Feature Extraction: In this method, new features are created by transforming or combining the original features. This process aims to capture the most significant information in fewer dimensions. Popular techniques include Principal Component Analysis (PCA) and Linear Discriminant Analysis (LDA).

Dimensionality reduction is vital in ensuring that the simplified data still represents the original patterns, making it easier to process and analyze.

Why use dimensionality reduction?

Dimensionality reduction offers several key benefits in machine learning:

• Avoiding the Curse of Dimensionality: As the number of dimensions (features) increases, data becomes sparse, making it difficult for models to learn and generalize. Reducing dimensions mitigates this issue, improving model performance.
• Reducing Model Complexity: By decreasing the number of features, dimensionality reduction simplifies models, leading to faster training and lower computational costs. It makes models less complex, which is beneficial for large datasets.
• Improving Model Performance: Fewer dimensions reduce the risk of overfitting, as models focus on the most relevant information. It also enhances accuracy by eliminating noise or irrelevant features.
• Facilitating Data Visualization: High-dimensional data is challenging to visualize. Dimensionality reduction techniques enable visualizing data in 2D or 3D, making it easier to identify patterns and insights.
• Saving Storage Space: Fewer dimensions mean smaller datasets, reducing storage requirements and making data handling more efficient

Why is Dimensionality Reduction important in Machine Learning and Predictive Modeling?

Dimensionality reduction plays a crucial role in various machine learning tasks like classification, regression, and clustering. Here’s why it’s important:

• Enhanced Interpretability: With fewer features, models become easier to interpret. Simplified models allow data scientists to understand and explain the impact of each variable, making decision-making more transparent.
• Improved Generalizability: Reducing the number of features helps in building models that generalize better to new, unseen data. It eliminates redundant or irrelevant information that might cause overfitting, ensuring that the model captures only the essential patterns.
• Optimized Performance: In predictive modeling, high-dimensional data can slow down computations and reduce efficiency. Dimensionality reduction techniques streamline the dataset, improving both training speed and prediction accuracy.
• Compatibility with Algorithms: Many algorithms work better with fewer dimensions. Dimensionality reduction ensures compatibility with such algorithms, enabling effective model building.

Dimensionality reduction not only simplifies the modeling process but also boosts performance, making it an essential step in machine learning​

Methods of Dimensionality Reduction

There are several popular methods for dimensionality reduction, each designed to simplify data while retaining its critical features. Here are some of the most widely used techniques:

1. Principal Component Analysis (PCA):

• PCA is a statistical technique that identifies the most informative components (features) in the data. It projects the data into a lower-dimensional space by finding directions (principal components) that maximize variance.
• This method is commonly used for data visualization and noise reduction as it effectively reduces dimensions while preserving the most significant information.

2. Linear Discriminant Analysis (LDA):

• LDA focuses on maximizing the separation between classes by finding a linear combination of features that best separates different classes.
• Unlike PCA, which is unsupervised, LDA requires class labels and is used mainly in classification tasks where distinguishing between categories is important.

3. t-Distributed Stochastic Neighbor Embedding (t-SNE):

• t-SNE is a nonlinear dimensionality reduction technique mainly used for visualizing high-dimensional data in a 2D or 3D space. It emphasizes maintaining the local structure of data, making clusters and patterns more visible.
• This method is often applied in exploratory data analysis and understanding data groupings.

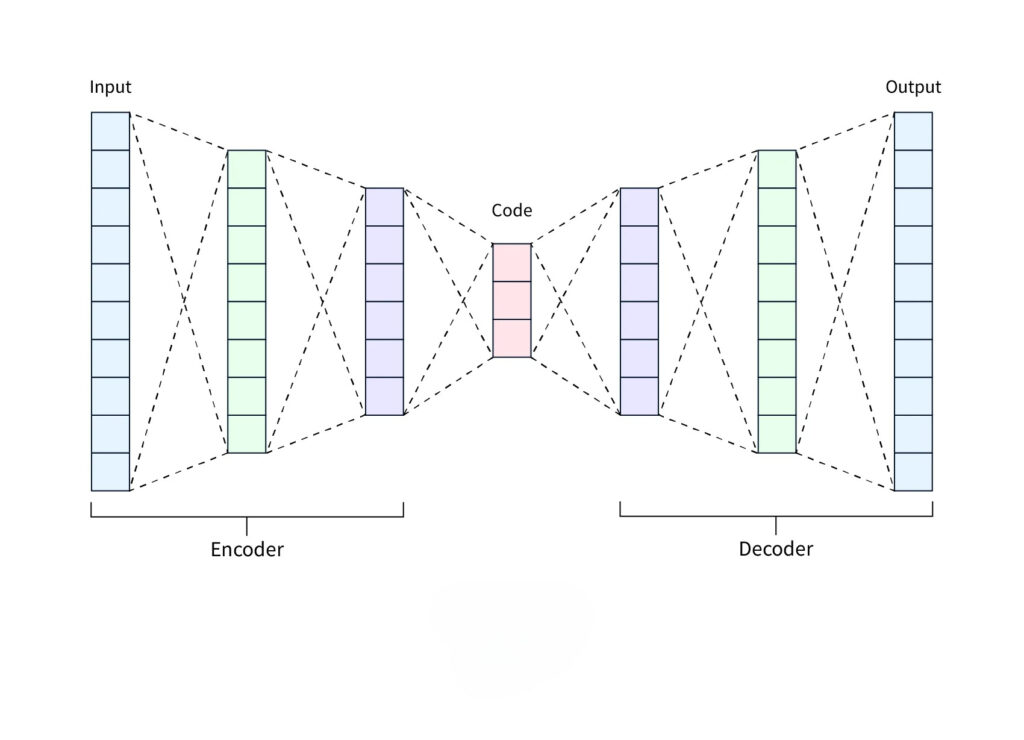
4. Autoencoders:

• Autoencoders are neural network-based models that learn to compress data into a lower-dimensional representation and then reconstruct the original data. They are particularly useful when dealing with complex, nonlinear data.
• Autoencoders offer flexibility and are often employed in deep learning applications where traditional methods may not perform well.

Each method has its advantages and is suitable for different scenarios, making it important to choose the right approach based on the type and structure of the data

Advantages of Dimensionality Reduction

Dimensionality reduction techniques offer several benefits in machine learning:

• Reduced Overfitting: By eliminating irrelevant features, dimensionality reduction helps models focus on the most important patterns, reducing the risk of overfitting and improving generalization to new data.
• Improved Model Efficiency: With fewer dimensions, models require less computational power and memory, making the training process faster and more efficient, especially for large datasets.
• Enhanced Data Visualization: Dimensionality reduction simplifies high-dimensional data, allowing for better visualization in 2D or 3D. This makes it easier to detect patterns, clusters, and trends that may not be visible in higher dimensions.
• Noise Reduction: Reducing dimensions also helps in removing noisy or redundant features, resulting in cleaner data that leads to more accurate models.

Disadvantages of Dimensionality Reduction

While dimensionality reduction has many benefits, it also comes with some drawbacks:

• Information Loss: Reducing dimensions may lead to the loss of some important information, which could affect the model’s performance or the accuracy of results. Finding the right balance between simplification and retaining essential data is crucial.
• Complexity in Choosing the Optimal Number of Dimensions: Deciding the appropriate number of dimensions to retain can be challenging. Keeping too many dimensions defeats the purpose, while reducing too many might eliminate critical information.
• Dependence on Data Distribution: Some dimensionality reduction techniques, such as PCA, assume that data is linearly separable. If the data has complex, nonlinear structures, these methods may not perform well, potentially leading to less effective results.
• Increased Computational Cost for Nonlinear Methods: Techniques like t-SNE and autoencoders, which are used for nonlinear data, can be computationally expensive and may require more time and resources compared to simpler linear methods.

Conclusion

Dimensionality reduction is a vital technique in machine learning, offering ways to simplify high-dimensional data while retaining important information. It enhances model performance, reduces computational complexity, and aids in data visualization, making it a powerful tool for data scientists. However, it’s essential to balance reducing dimensions and retaining crucial details to avoid information loss. By understanding and applying dimensionality reduction techniques appropriately, one can optimize models and improve the overall efficiency of machine learning workflows.