Bias and Variance in Machine Learning

Machine learning models aim to make accurate predictions by learning from data. However, two critical factors—bias and variance—affect the performance of these models. Understanding and balancing these factors is essential for building models that generalize well to new data. Bias refers to errors due to overly simplistic assumptions in the learning algorithm, while variance measures the model’s sensitivity to fluctuations in the training data. Striking the right balance between bias and variance is key to minimizing model errors and improving accuracy.

In this article, we’ll explore the concepts of bias and variance, how they influence model performance, and practical strategies for reducing both to build robust machine learning models.

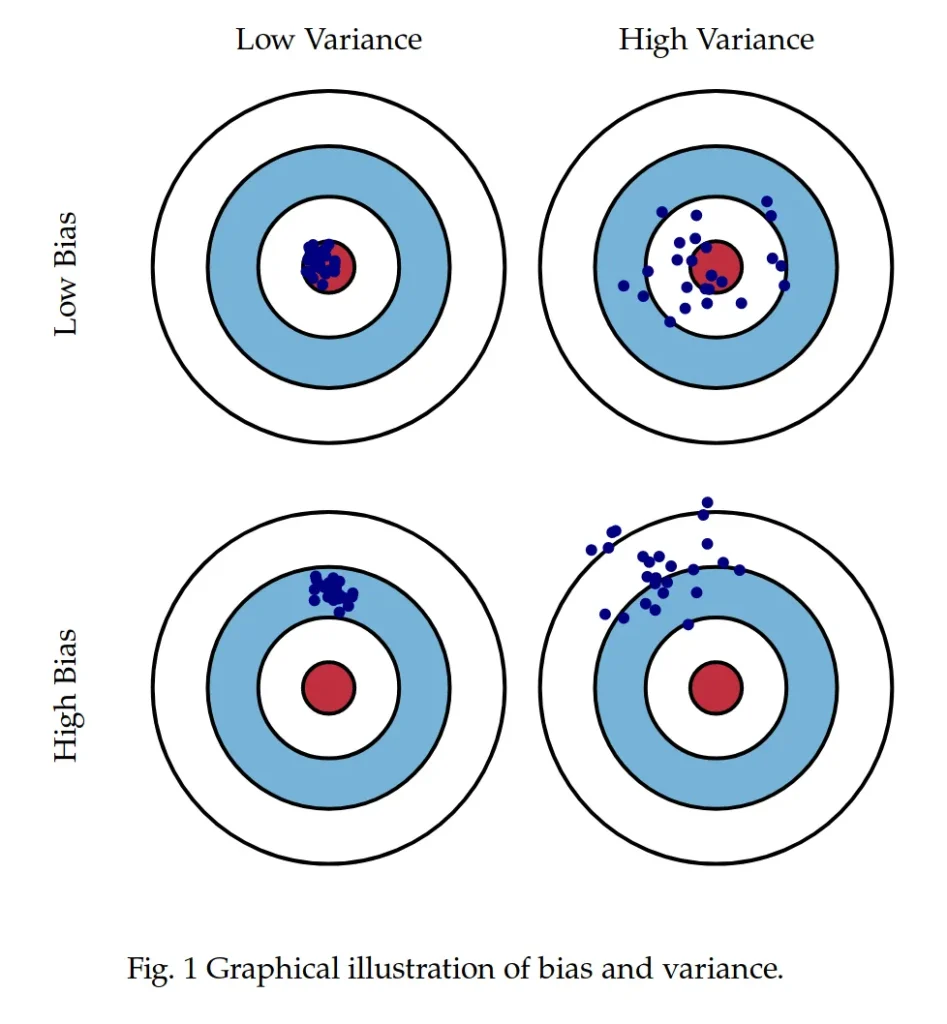
What is Bias in Machine Learning?

Bias in machine learning refers to the error introduced by approximating a real-world problem, which may be complex, using a simplified model. It arises when the assumptions made by the model are too rigid, leading to oversimplifications. Models with high bias tend to underfit the data, meaning they fail to capture the underlying patterns in the dataset.

Low Bias vs. High Bias

• Low Bias: A low-bias model generally fits the training data well because it can capture complex relationships in the data. However, this doesn’t guarantee good performance on unseen data. A low-bias model might still overfit the training data if variance is too high.
• High Bias: A model with high bias tends to be overly simplistic, assuming a linear relationship when the data might be more complex. For example, if you’re using a linear regression model for non-linear data, it could result in high bias, which leads to underfitting.

Example: Imagine trying to predict house prices using only one feature, such as the square footage. The model might ignore other important factors like location or the number of bedrooms, leading to high bias and poor performance.

Impact of Bias on Model Performance

High bias affects the model’s ability to generalize from the training data. If a model underfits, it will perform poorly on both the training data and new, unseen data. A high-bias model fails to learn the true relationships in the data, producing predictions that are consistently off the mark.

Ways to Reduce High Bias in Machine Learning

Reducing bias is essential for improving the accuracy of machine learning models, especially when underfitting occurs. Here are several strategies to address high bias:

1. Use a More Complex Model

One of the most effective ways to reduce bias is by using a more complex model that can capture the intricate relationships within the data. For instance:

• Decision Trees and Deep Learning models can learn non-linear relationships, unlike simpler models like linear regression.
• However, while a more complex model can reduce bias, it can also introduce higher variance, so it’s essential to monitor the trade-off between bias and variance carefully.

2. Increase the Number of Features

Sometimes, the issue of high bias arises because the model lacks enough relevant features to accurately represent the underlying patterns in the data. Including additional, meaningful features allows the model to learn more intricate patterns. For example:

• A model predicting house prices might perform better if it considers features like the neighborhood, year built, and number of bedrooms in addition to square footage.
• Feature selection is still important to avoid adding irrelevant data, which might increase the complexity unnecessarily and lead to overfitting.

3. Reduce Regularization

Regularization techniques like L1 and L2 penalties are often used to prevent overfitting by reducing model complexity. However, if regularization is too strong, it can introduce bias by overly simplifying the model. Adjusting the regularization strength can help:

• Reduce regularization slightly to allow the model to capture more patterns from the data.
• This adjustment should be carefully balanced to avoid increasing the risk of overfitting.

4. Increase the Size of the Training Data

A larger dataset allows the model to better learn the underlying patterns, reducing bias. When more training data is available, the model can differentiate between real patterns and random noise more effectively. If obtaining more data is challenging, data augmentation techniques can be used to artificially expand the dataset.

Example: In image classification tasks, augmenting images by rotating, flipping, or adjusting brightness can provide additional data points, helping to improve the model’s performance and reduce bias.

What is Variance in Machine Learning?

Variance in machine learning refers to the model’s sensitivity to small fluctuations in the training data. High variance occurs when a model captures not only the underlying patterns but also the noise in the training data, leading to overfitting. This means that while the model performs well on the training set, its performance on unseen data can degrade significantly.

Low Variance vs. High Variance

• Low Variance: A low-variance model tends to generalize well but may underfit the data if its bias is too high. Such a model may overlook complex relationships within the data.
• High Variance: High-variance models are prone to overfitting, as they adapt too closely to the specific data points in the training set, including noise. This leads to a model that performs well on the training data but struggles with generalization, meaning it will perform poorly on new data.

Example: Consider a decision tree with many branches and splits that perfectly fits the training data. While this tree may predict the training data with great accuracy, it might fail to generalize when tested on unseen data, as it has “memorized” the training set rather than learning the general patterns.

Impact of Variance on Model Performance

High variance results in a model that is overly complex and fails to generalize. While it can achieve excellent accuracy on the training data, the performance on test data will be significantly lower, leading to poor generalization. High variance can be particularly problematic when dealing with small datasets, as the model may pick up random noise and mistake it for significant patterns.

Ways to Reduce Variance in Machine Learning

To improve a model’s generalization ability and reduce variance, various techniques can be employed. Here are some common strategies:

1. Cross-Validation

Cross-validation is a powerful technique for reducing variance and avoiding overfitting. It works by dividing the dataset into multiple subsets, training the model on some subsets while validating it on others.

• K-Fold Cross-Validation is one of the most popular approaches. The data is split into ‘K’ number of folds, and the model is trained and tested on each fold. This helps in ensuring that the model performs consistently across different subsets of the data, making it less likely to overfit to any one subset.

2. Feature Selection

Reducing the number of irrelevant or noisy features can help decrease variance. Irrelevant features often introduce noise into the model, causing it to overfit the training data.

• Feature selection techniques, such as Recursive Feature Elimination (RFE) and Principal Component Analysis (PCA), can be employed to identify the most relevant features and remove the unnecessary ones.
• By focusing on the key features, the model becomes simpler and less sensitive to noise, which reduces overfitting.

3. Regularization

Regularization techniques such as L1 (Lasso) and L2 (Ridge) penalize overly complex models, discouraging the model from fitting the noise in the training data. Regularization can be a powerful tool for controlling the complexity of models like neural networks and logistic regression.

• L2 Regularization works by adding a penalty proportional to the square of the magnitude of the coefficients.
• L1 Regularization adds a penalty proportional to the absolute value of the coefficients, effectively leading to sparse models by driving some coefficients to zero.

By controlling complexity, regularization can prevent the model from capturing noise, thereby reducing variance.

4. Ensemble Methods

Ensemble methods combine predictions from multiple models to reduce overall variance. These models average out individual errors, leading to a more robust and generalizable solution.

• Bagging (e.g., Random Forests) reduces variance by training multiple models on different subsets of the data and averaging their predictions.
• Boosting (e.g., Gradient Boosting) reduces both bias and variance by sequentially training models, where each model corrects the errors of its predecessor.

Ensemble methods are especially effective in reducing the variance of high-variance models like decision trees.

5. Simplifying the Model

In some cases, reducing model complexity by using a simpler algorithm can decrease variance. For example, switching from a complex decision tree to a linear regression model might lead to better generalization, particularly when the dataset is small or the problem is relatively straightforward.

• However, simplifying the model too much may introduce bias, so it’s essential to find the right balance.

6. Early Stopping

In iterative learning processes, such as training deep learning models, early stopping can be an effective technique to prevent overfitting. By monitoring the performance of the model on a validation set during training, the process can be halted when the validation error starts increasing, indicating that the model is beginning to overfit the training data.

• This prevents the model from becoming too complex and ensures it generalizes better to unseen data.

Mathematical Derivation for Total Error

The total error in a machine learning model can be understood as the sum of three main components: bias, variance, and irreducible error. The formula is:

Total Error=Bias2+Variance+Irreducible Error

• Bias represents the error due to the model’s simplifying assumptions. High bias leads to underfitting.
• Variance represents how much the model’s predictions change when different training data is used. High variance leads to overfitting.
• Irreducible Error is the error inherent in the problem itself that cannot be reduced, even with a perfect model (e.g., noise in the data).

This equation shows how increasing one component (bias or variance) decreases the other, making it important to find the right balance.

Different Combinations of Bias-Variance

Different combinations of bias and variance lead to varying model performance. Let’s discuss the most common scenarios:

1. High Bias, Low Variance

• Characteristics: A model with high bias makes strong assumptions about the data and is likely too simplistic to capture the underlying patterns. However, it is stable across different datasets, leading to low variance.
• Implications: High-bias models tend to underfit, meaning they perform poorly on both training and test data.
• Example: Linear regression used on a non-linear dataset.

2. Low Bias, High Variance

• Characteristics: A model with low bias can fit the training data well, capturing complex relationships. However, it becomes overly sensitive to fluctuations in the training data, resulting in high variance.
• Implications: Low-bias, high-variance models tend to overfit, performing well on training data but poorly on new, unseen data.
• Example: A deep decision tree that perfectly fits the training data but performs poorly on test data.

3. High Bias, High Variance

• Characteristics: A model that is both overly simplistic and unstable across datasets suffers from both high bias and high variance. This is the worst-case scenario as it both underfits and fails to generalize.
• Implications: These models perform poorly on all data.
• Example: An under-regularized model with limited features.

4. Low Bias, Low Variance

• Characteristics: This is the ideal situation, where the model generalizes well, capturing the right patterns without being too sensitive to the specific data used in training.
• Implications: Low-bias, low-variance models tend to generalize well and perform consistently across both training and test datasets.
• Example: Random Forests or models that achieve the right balance through techniques like cross-validation and regularization.

Bias Variance Tradeoff

The bias-variance tradeoff refers to the balance between the two sources of error—bias and variance—in a machine learning model. Optimizing this tradeoff is crucial for building models that generalize well to new data.

• High Bias, Low Variance: As seen earlier, models with high bias make strong assumptions about the data, often oversimplifying and underfitting. They may be consistent across different datasets (low variance), but they perform poorly on both training and test data.
• Low Bias, High Variance: On the other hand, models with low bias can learn the training data well, but they become too sensitive to noise in the data, leading to overfitting and poor generalization (high variance).

The goal is to find a sweet spot between bias and variance, where the model is complex enough to capture the underlying patterns in the data but not so complex that it overfits. This sweet spot often involves some trade-off, as reducing one type of error usually increases the other.

Practical Example of Bias-Variance Tradeoff

In practice, you may start with a simple model like linear regression, which has high bias but low variance. If it underfits, you can move to a more complex model, such as a polynomial regression or decision tree. These models reduce bias by fitting the data more accurately, but at the cost of increasing variance.

Regularization techniques, cross-validation, and ensemble methods can help strike the right balance between bias and variance by reducing model complexity or stabilizing predictions across different data subsets.

Bias Variance Decomposition for Classification and Regression

Bias-variance decomposition applies differently to classification and regression tasks. In both cases, the goal is to minimize the error caused by both bias and variance, but the models and techniques used to address these errors may vary slightly.

Let’s take a look at how bias and variance affect both classification and regression models using a code example.

Bias-Variance Decomposition in Regression

In this example, we’ll use polynomial regression with varying degrees of complexity to illustrate how bias and variance affect the model.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split

# Generate random data
np.random.seed(0)
X = np.sort(5 * np.random.rand(80, 1))
y = np.sin(X).ravel()
y[::5] += 1 * (0.5 - np.random.rand(16))  # Adding some noise

# Split data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Fit polynomial regression models of varying degrees (1, 4, and 15)
degrees = [1, 4, 15]
plt.figure(figsize=(12, 6))

for i, degree in enumerate(degrees):
    poly = PolynomialFeatures(degree=degree)
    X_poly_train = poly.fit_transform(X_train)
    X_poly_test = poly.transform(X_test)

    # Train the model
    model = LinearRegression()
    model.fit(X_poly_train, y_train)

    # Predict on the test set
    y_pred = model.predict(X_poly_test)

    # Calculate Mean Squared Error (MSE)
    mse = mean_squared_error(y_test, y_pred)
    print(f'Degree {degree}: Mean Squared Error = {mse:.3f}')

    # Plot the results
    X_plot = np.linspace(0, 5, 100).reshape(-1, 1)
    y_plot = model.predict(poly.transform(X_plot))

    plt.subplot(1, 3, i + 1)
    plt.scatter(X_train, y_train, color='black', label='Training Data')
    plt.plot(X_plot, y_plot, label=f'Degree {degree}', color='red')
    plt.legend()
    plt.title(f'Degree {degree}\nMSE: {mse:.3f}')
    plt.xlabel('X')
    plt.ylabel('y')

plt.tight_layout()
plt.show()

Explanation:

• Degree 1 (Linear Regression): This model has high bias, underfitting the data as it is too simplistic to capture the complex non-linear relationship. The error will be relatively high due to underfitting.
• Degree 4 (Moderate Complexity): This model strikes a balance between bias and variance. It captures the underlying patterns without overfitting or underfitting the data.
• Degree 15 (High Complexity): This model has high variance, overfitting the training data by capturing even the noise, leading to poor generalization on the test data.

Output (Sample MSE values):

Degree 1: Mean Squared Error = 0.580
Degree 4: Mean Squared Error = 0.152
Degree 15: Mean Squared Error = 1.345

The plot will show how the model becomes more complex as the degree increases, with Degree 15 overfitting the training data but performing poorly on unseen data.

Bias-Variance Decomposition in Classification

For classification, let’s use a decision tree model on a sample dataset to illustrate bias and variance in classification tasks.

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# Load the Iris dataset
iris = load_iris()
X, y = iris.data, iris.target

# Split into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Train decision tree classifiers with different depths
depths = [1, 5, 10]
for depth in depths:
    tree = DecisionTreeClassifier(max_depth=depth, random_state=42)
    tree.fit(X_train, y_train)
    
    # Predict and evaluate
    y_pred_train = tree.predict(X_train)
    y_pred_test = tree.predict(X_test)
    train_acc = accuracy_score(y_train, y_pred_train)
    test_acc = accuracy_score(y_test, y_pred_test)
    
    print(f"Depth {depth}: Train Accuracy = {train_acc:.3f}, Test Accuracy = {test_acc:.3f}")

Explanation:

• Depth 1 (High Bias): A very shallow tree that oversimplifies the problem, leading to underfitting (high bias).
• Depth 5 (Balanced): A moderately complex tree that finds a good balance between bias and variance, leading to good performance on both training and test sets.
• Depth 10 (High Variance): A deep tree that overfits the training data by learning every detail, resulting in high variance and poor generalization.

Output (Sample accuracy values):

Depth 1: Train Accuracy = 0.643, Test Accuracy = 0.600
Depth 5: Train Accuracy = 0.971, Test Accuracy = 0.933
Depth 10: Train Accuracy = 1.000, Test Accuracy = 0.911

This demonstrates how increasing the depth of the tree can lead to overfitting (high variance), even though it may perform well on the training set.

Considering Bias and Variance is Crucial

In machine learning, carefully balancing bias and variance is crucial for developing models that generalize well to unseen data. Focusing on one without considering the other can lead to poor model performance.

• High Bias models, as we’ve seen, are overly simplistic and result in underfitting. These models fail to capture the complexities of the data, which leads to poor predictive performance on both training and test datasets.
• High Variance models, on the other hand, are overly complex and tend to overfit the training data. While these models may achieve high accuracy on the training set, they fail to generalize to new data, resulting in poor test performance.

Key Takeaways:

• Understanding the Bias-Variance Tradeoff: Every machine learning model needs a balanced approach to bias and variance. Reducing one often increases the other, so achieving the right balance is critical to minimizing total error.
• Regular Monitoring: During model development, it is essential to evaluate performance on both training and validation sets to monitor bias and variance. Techniques like cross-validation can help identify and address overfitting or underfitting early on.
• Choosing the Right Model: Different algorithms inherently have different levels of bias and variance. For instance, simpler models like linear regression tend to have higher bias and lower variance, while more complex models like deep learning may have lower bias but higher variance. Choosing the appropriate model based on the problem at hand is critical.
• Applying Techniques to Control Bias and Variance: Regularization, feature selection, ensemble methods, and cross-validation are all useful techniques to manage the tradeoff between bias and variance, ensuring that the model performs well on both training and unseen data.

The ability to strike the right balance between bias and variance directly impacts the accuracy, reliability, and generalization of machine learning models.